Consulta todos los tipos de arreglos en programación. Para entender las diversas utilidades en programación, resulta esencial conocer los distintos tipos de estructuras de datos que existen, como son los arreglos o arrays. Si tienes alguna inquietud recuerda contactarnos a través de nuestras redes sociales, o regístrate y déjanos un comentario en esta página. También puedes participar en el WhatsApp. Si usas Telegram ingresa al siguiente enlace.

Consulta todos los tipos de arreglos en programación

En la informática, cuando se habla de un arreglo o array, nos referimos a una estructura de datos que contiene un grupo de elementos, normalmente del mismo tipo, que se almacenan en posiciones contiguas de memoria.

Los arreglos permiten acceder a cualquier dato a través de un índice o ubicación. Por ejemplo, si se tiene un array de 5 números, para acceder a cada número, se indica la posición que se busca en el arreglo.

¿Qué es un arreglo?

La principal característica de los arreglos es que sus elementos se guardan y ejecutan directamente en la memoria RAM del ordenador. Ellos gestionan funciones de carácter temporal, y a través de su manipulación es posible cambiar los valores almacenados en el array.

Pueden variar según la lógica de programación aplicada. Algunos pueden contener elementos solo de un mismo tipo, mientras que otros albergan datos de diferentes tipos. No obstante, independientemente de su composición, los arreglos sirven como contenedores de información.

Una ventaja notable de los arreglos es su flexibilidad. Permiten realizar combinaciones para optimizar su estructura, lo que genera mayor estabilidad y velocidad en el procesamiento de información.

En ocasiones, al manipular arreglos de códigos, estos se ejecutan cíclicamente, lo que quiere decir que los datos modificados deben completar todo el proceso para asegurar la efectividad del cambio.

Asimismo, los arreglos se comparan con las matrices y vectores que se estudian en las ciencias puras. Ambos solucionan problemas mediante algoritmos, lo que les otorga un papel crucial en la programación.

Los arreglos pueden tener diferentes dimensiones. Por lo general, se clasifican en tres categorías principales, según el número de dimensiones:

• Vectores: Son arreglos de una dimensión. Cada elemento en el vector se puede acceder mediante un único índice.
• Matrices: Son arreglos de dos dimensiones. Para acceder a un elemento en una matriz, se necesitan dos índices, uno para la fila y otro para la columna.
• Tablas Multidimensionales: Son arreglos de tres o más dimensiones. Cada elemento en la tabla se puede acceder mediante tres o más índices.
• Es importante mencionar que los programadores deben trabajar dentro de ciertos límites al manipular arreglos. En caso de que se violen estas restricciones, hay un alto riesgo de que los códigos de array fallen, lo que puede comprometer todo el programa. En tales casos, es común ver mensajes de error de sintaxis, lo que indica que los códigos no coinciden o que existen elementos no apropiados en el arreglo.

Tipos

Los arreglos son estructuras de datos que almacenan una colección ordenada de elementos del mismo tipo. Se utilizan para manejar grandes cantidades de información de forma organizada y eficiente. Los arreglos son los equivalentes en programación de las matrices y vectores de las matemáticas.

Dependiendo de la cantidad de dimensiones y del número de usos, entonces los arreglos se pueden clasificar en tipos y forma. De esta manera podemos estructurar las cualidades que tendrá durante la ejecución, evitando potenciales errores durante la lectura de datos.

Los arreglos se pueden crear y manipular usando el módulo NumPy , que provee las estructuras de datos y las funciones para trabajar con arreglos. Para usar las funciones provistas por NumPy, debemos importarlas al principio del programa: from numpy import *.

Los valores dentro del arreglo inician en cero, y siempre culminan en n-1, donde n significa el tamaño del componente. Además, a pesar de estar dividido en una clasificación ellos poseen varias características en común:

• Poseen un nombre en común, que los representa a todos y a cada variable que lo integra, sin embargo, se distinguen por su índice.
• Cada valor registrado dentro del arreglo se almacena en una memoria de acuerdo a la posición que tenga dentro del sistema.
• A pesar de pertenecer a celdas, por así decirlo, el programador puede acceder a ellos de dos maneras: directa o aleatoriamente.

Arreglos Unidimensionales

Se le llama así al arreglo que tiene una sola dimensión o eje. Es decir, es una secuencia lineal de elementos que se pueden acceder mediante un solo índice. Se le podría considerar un vector, y por ende solo cuenta con una lista de datos que pueden ubicarse a través de un valor que indica su puesto dentro del arreglo.

Para crear un arreglo unidimensional nuevo, se puede usar la función array pasándole como parámetro la lista de valores que deseamos agregar al arreglo: a = array( [6, 1, 3, 9, 8]). Todos los elementos del arreglo tienen exactamente el mismo tipo. Para crear un arreglo de números reales, basta con que uno de los valores lo sea: b = array( [6.0, 1, 3, 9, 8]). Otra opción es convertir el arreglo a otro tipo usando el método astype: a.astype(float).

Arreglos Multidimensionales

Se le llama así al arreglo que tiene más de dos dimensiones o ejes. Es decir, es una estructura de datos más compleja que puede representar sistemas del mundo real con mayor detalle. Los arreglos multidimensionales se pueden acceder mediante tantos índices como dimensiones tenga el arreglo.

Para crear un arreglo multidimensional nuevo, se puede usar la función array pasándole como parámetro una lista anidada que represente las dimensiones del arreglo: e = array( [[[1, 2], [3, 4]], [[5, 6], [7, 8]]]).

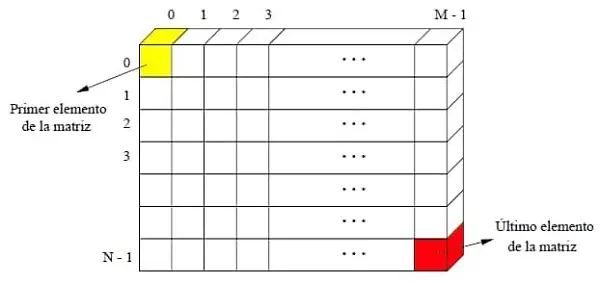
Este ejemplo crea un arreglo tridimensional con dos filas, dos columnas y dos capas. Todos los elementos del arreglo tienen exactamente el mismo tipo. Para crear un arreglo de números reales, basta con que uno de los valores lo sea: f = array( [[[1.0, 2], [3, 4]], [[5, 6], [7, 8]]]). Otra opción es convertir el arreglo a otro tipo usando el método astype: e.astype(float).

Arreglos de múltiples Índices

Se conforma por filas y columnas especiales, que debido a la complejidad de su diseño tienen la capacidad de encontrar un dato sin importar el número de códigos que tenga alrededor.

Ahora bien, en cuanto a su funcionamiento las líneas de códigos se comportan de la siguiente manera: En primer lugar, se realiza la lectura de los primeros datos, allí se inicia la búsqueda del índice que se desea encontrar dentro del arreglo, mientras que al mismo tiempo otra serie de algoritmos indagan dentro de una columna otro lote de información.

Es importante tomar en cuenta, que este tipo de arreglos múltiples basan su diseño en el modelo conocido como ANSI, que es usado en todo el mundo. Y que estipula que cualquier arreglo similar a este, debe apegarse al uso de dos índices de códigos es un mismo momento, para evitar un desequilibrio en el sistema y con la información.

Clasificación

Los arreglos se clasifican según el número de dimensiones que tengan, es decir, el número de subíndices que se necesitan para referirse a un elemento particular en el arreglo. Los que de más de una dimensión se llaman arreglos multidimensionales. A continuación se describen los tres tipos más comunes de arreglos:

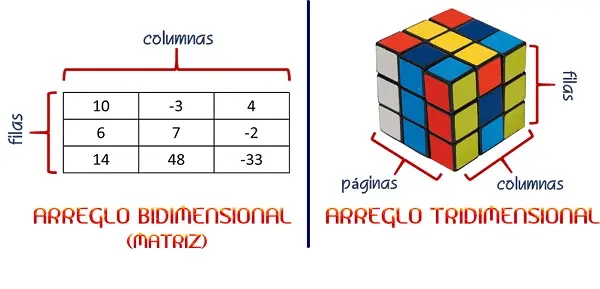
Vectores

Se le conoce como vectores, aunque en lenguaje de programación son conocidos como Arreglos Unidimensionales, ya que poseen una única dimensión.

¿Eso qué significa? que solo requieren de un subíndice para identificar un elemento en el arreglo, creando de esa forma ciclos simples y breves que no tienen ningún tipo de complejidad para el desarrollo de cada una de sus tareas.

Sin embargo, para que esto ocurra los datos alojados en su núcleo deben ser del mismo tipo y tamaño, por lo regular es numérico. Además, a pesar de su similitud deben diferenciarse bajo un distinto número de posición y así como de un valor, para que el algoritmo pueda distinguirse de otro.

Pero no solo eso, otra peculiaridad es que los datos se organizan de forma consecutiva en la memoria, y los ciclos arrancan desde la posición cero hasta la última posición del arreglo. Lo que significa, que los datos más pequeños serán siempre los primeros en leerse bajo el vector del sistema, dejando de último los valores más altos.

Ahora bien, en cuanto a su composición ellos se agrupan mediante una serie de valores, los cuales tienen una posición que es marcada por el vector en el que se alojan.

Matrices

Por lo regular son conocidas como Matrices o Arreglos Bidimensionales, poseen dos dimensiones dentro de la estructura del sistema. Pero no solo eso, los datos son diseñados para tener rasgos similares a los vectores, de esa forma se crea un funcionamiento equilibrado y eficiente.

Pero como estamos ante un índice de 2 dimensiones, significa entonces que la línea de código se maneja bajo dos tipos de subíndices, que son aquellos que realizan las tareas programadas de una manera más compleja que el caso anterior.

Además, los datos que se alojen a este tipo de diseño deben ser clasificados e inicializados bajo una identificación única. ¿Qué significa esto? pues que cada dato se registra por cuadrante, y el mismo es ubicado bajo una serie de coordenadas de posición.

Recordemos lo mencionado con anterioridad, que cada dato se clasifica por dimensiones, y como estamos ante una matriz significa entonces que tendremos la misma cantidad de filas que de columnas.

Tablas Multidimensionales

Este último arreglo al igual que el caso anterior, cuenta con un diseño complejo en su núcleo, con la diferencia de tener 3 dimensiones en vez de 2.

Esto en sencillas palabras significa más subíndices, más datos y más procesamiento de información. Sin embargo, debido al enorme lote de códigos es obligatorio que cuenten con la aclaración de su tamaño, forma y tipo para evitar errores durante la programación de los especialistas.

Las tablas multidimensionales se pueden visualizar como cubos o hipercubos de información, donde cada dimensión del cubo corresponde a un campo de dimensiones en la tabla, y la información almacenada en cada celda del cubo corresponde a las medidas.

Estos cubos permiten realizar análisis OLAP (On-Line Analytical Processing), que consiste en aplicar operaciones como filtrar, ordenar, agrupar, sumarizar y pivotar los datos para obtener diferentes perspectivas y extraer conocimiento.

Se utilizan principalmente para crear aplicaciones de Data Warehouse o almacenes de datos, que son sistemas que integran datos provenientes de diversas fuentes y los organizan por temas para facilitar su consulta y análisis. Las tablas multidimensionales también se pueden construir a partir de otras bases de datos relacionales, mediante procesos de transformación y carga (ETL) que extraen los datos de las tablas originales y los adaptan al formato multidimensional.

Operaciones con arreglos

Cualquier programa, aplicación y todo tipo que cuente con un sistema de información puede ser propensas a sufrir algún tipo de arreglo para seguir ejerciendo sus funciones.

Esto debido a muchos factores, pero por lo general se debe a que solo se reflejan los datos pero los mismos no son alojados en ningún tipo de memoria, o que son usados para otra cadena de códigos que no sean los suyos.

Los arreglos cuando se encuentran en funcionamiento, son almacenados temporalmente en alguna fuente como la memoria RAM, ya que estos se ubican en en el núcleo central del programa.

Que en palabras sencillas significa que los arreglos cuando se encuentran inactivos, los mismos se alojan en la fuente raíz del sistema, y al activarlos lo único que varía es que la información es enviada a la memoria temporal.

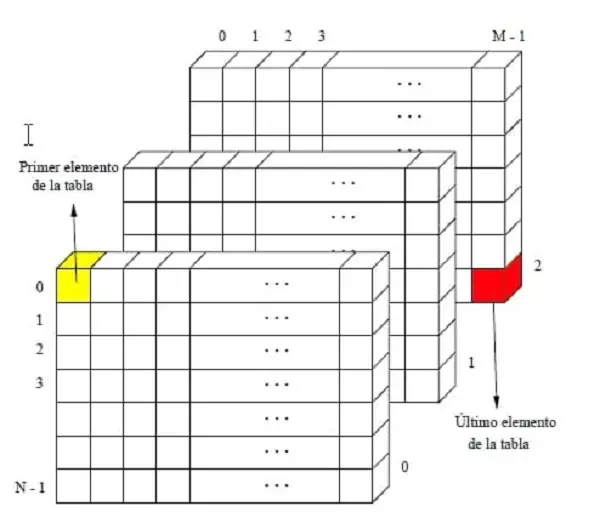
En ninguna oportunidad se pierde información, sin embargo siempre se debe configurar bien el tipo de tarea que se quiere realizar. Pero además de eso el programador debe siempre informar el tipo de arreglo que está realizando, así como la cantidad de filas y columnas que tendrá al terminar.

Ahora bien, sobre un arreglo se pueden hacer distintos tipos de operaciones, que dependiendo de lo que se requiera puede tener cualquiera de estas estructuras:

• Ingresar
• Sumar y Promedio
• Mayor y Menor
• Buscar y Reemplazar
• Ordenar e Invertir
• Insertar y Eliminar

Ahora bien, para poder aplicar las soluciones a dichos arreglos se debe considerar varias cosas: Primero si la falla es demasiado grande, entonces las operaciones se subdividen y se realiza un análisis, un diseño y se implementa luego por separado para formar un solo array. Para ello, debemos saber lo siguiente:

• Arreglo: variable para manipular el arreglo
• Tamaño: cantidad máxima de datos del arreglo
• Indexado: posición inicial del arreglo
• Ya en este punto deberíamos conocer de manera más sencilla el significado de un array y la forma en la que operan, todo esto de acuerdo a la programación.

Sin embargo, como estamos ante diversos tipos de arreglos en programación, significa entonces que hay mucho más por conocer, como por ejemplo las funciones que son capaces de realizar como conjuntos de datos.

Por lo tanto, existen cientos de posibilidades con los arrays, lo único que hace falta es conocer bien su estructura para dar el siguiente paso: que es programar.